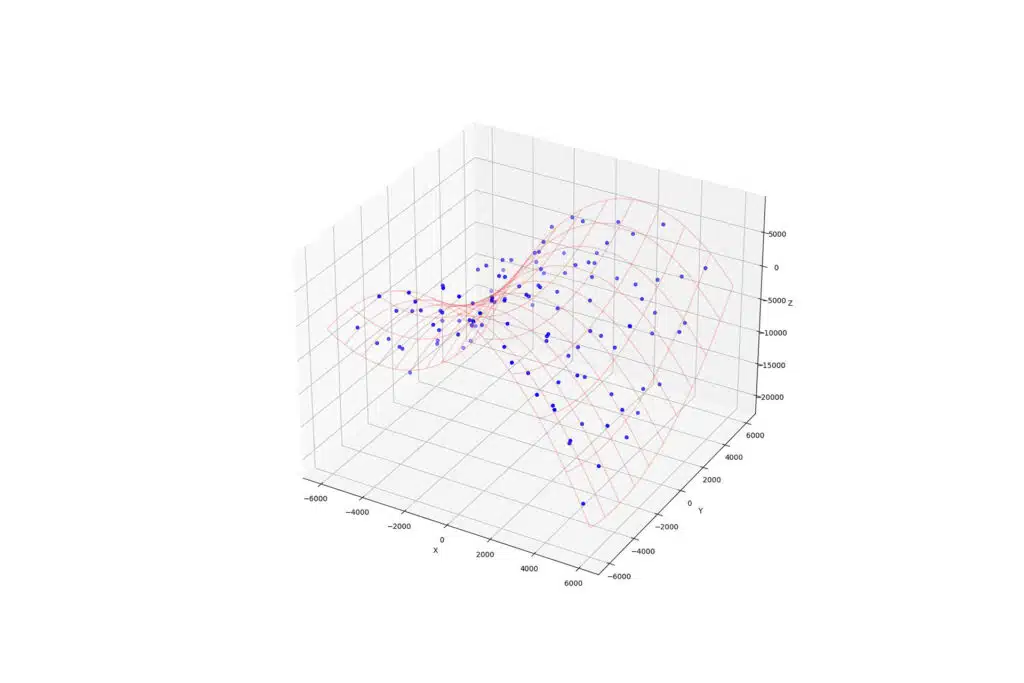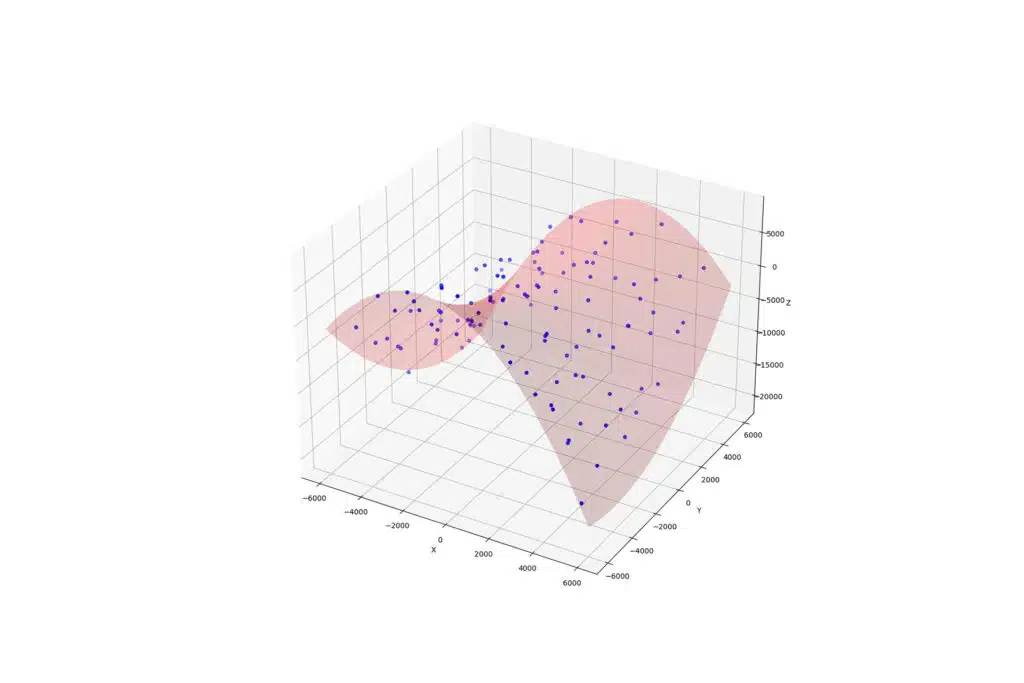
工作上的事情還真是無奇不有,什麼工具都得會一點才行。在這個例子中,共有100組數據存放在data.csv裡,每一組數據(每一列)包含x座標、y座標與對應的數值z,依序放在data.csv檔裡的前三欄,data.csv的內容如下
x,y,z
-5366.14,-4776.75,-2053.64
-5148.93,-3732.71,-5843.89
-5286.6,-2664.6,-7058.72
-4877.6,-2495.51,-8136.17
-5157.85,-1314.45,-14301.11
...
4983.15,3716.11,-5360.5
5228.11,4954.56,1150.98
本次的需求是要找出一個曲面去擬合這100組數據,所以先利用pandas套件iloc的功能把csv檔的內容讀進來並利用numpy套件將其合併成一個二維numpy陣列,方便後續的運算和處理。
import pandas as pd
import numpy as np
df = pd.read_csv('data.csv')
x = df.iloc[:, 0]
y = df.iloc[:, 1]
z = df.iloc[:, 2]
data = np.array([x, y, z]).T
df.iloc[:, n] 從df中選擇所有的行(冒號表示選擇所有行),並選擇第n列的數據。
np.array([x, y, z]).T 將x、y和z三個一維數列合併成二維陣列並轉置,此時data的內容為
[[ -5366.14 -4776.75 -2053.64]
[ -5148.93 -3732.71 -5843.89]
[ -5286.6 -2664.6 -7058.72]
[ -4877.6 -2495.51 -8136.17]
[ -5157.85 -1314.45 -14301.11]
...
[ 4983.15 3716.11 -5360.5 ]
[ 5228.11 4954.56 1150.98]]
再來定義一個擬合曲面fit_equation並利用scipy的curve_fit找出擬合曲面中每一項的係數
from scipy.optimize import curve_fit
def fit_equation(xy, a, b, c, d, e, f):
x, y = xy
return a*x + b*y + c*x*x + d*y*y + e*x*y + f
popt, pcov = curve_fit(fit_equation, (x, y), z)
print(popt)
popt包含了每一項的最佳擬合係數,它讓我們定義的擬合曲面fit_equation與實際數據擬合出最好的結果,而pcov是協方差矩陣,它提供了popt各係數的不確定性估計。
print(popt)可以把每一項的係數給列出來,結果如下
[ 2.31992768e-02 -1.45919396e-01 -4.64725528e-04 1.73354088e-04
2.46451189e-04 -5.35930627e+01]
如果不要以科學記號表示,且只取小數點下八位的話,加上
np.set_printoptions(suppress=True, precision=8)
這樣可以得到
[ 0.02319928 -0.1459194 -0.00046473 0.00017335 0.00024645
-53.59306267]
如果需要將數據點與擬合曲面做繪圖的話,利用pyplot套件
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, color='blue')
x_r = np.linspace(-6000, 6000, 100)
y_r = np.linspace(-6000, 6000, 100)
X, Y = np.meshgrid(x_r, y_r)
Z = fit_equation((X, Y), *popt)
ax.plot_surface(X, Y, Z, color='red', alpha=0.2)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
fig = plt.figure() 建立一個新的Matplotlib容器。
ax = fig.add_subplot(111, projection=’3d’) 在fig上增加一個3D subplot。111 的意思是將圖分為1行1列,並在第1個位置新增subplot,而projection=’3d’則表示我們要使用3D的投影方式。
ax.scatter(x, y, z, color=’blue’) 在建立的3D subplot上繪製分佈圖,color=’blue’指定數據點以藍色顯示。
x_r = np.linspace(-6000, 6000, 100) 繪製曲面的參數,其限制座標軸x範圍為-6000至6000,並在-6000至6000之間均勻置入 100 個點。若置入的點數愈多,繪製出來的曲面愈平滑,下圖分別為點數2、3、5和100所繪製出的曲面。
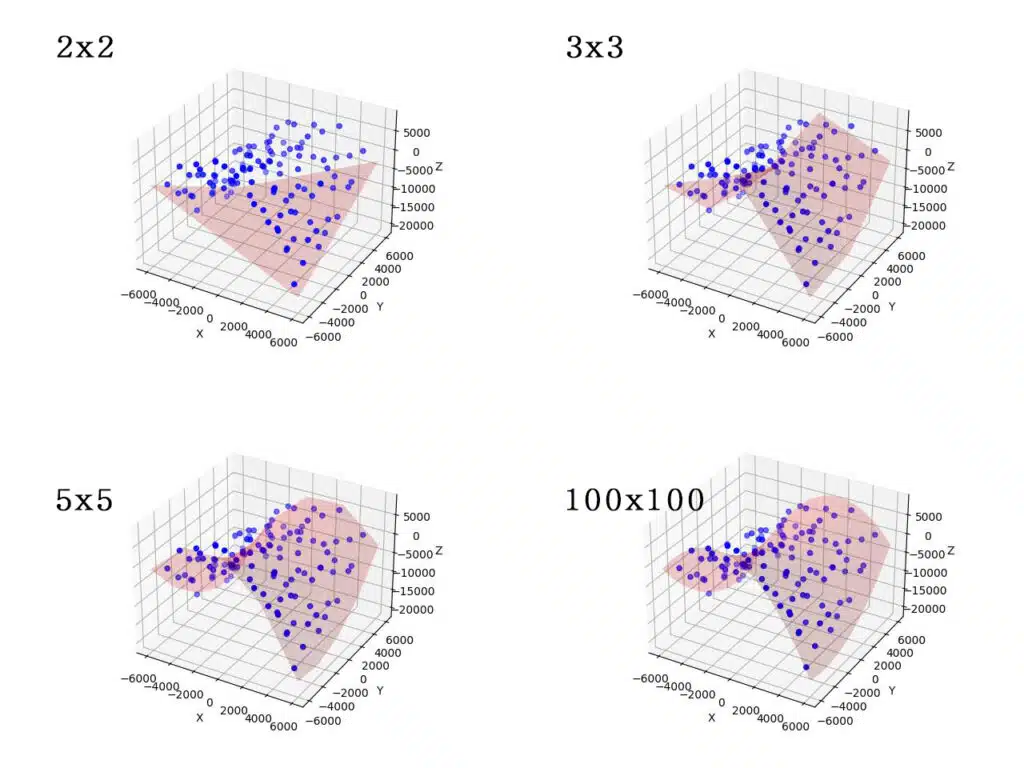
y_r = np.linspace(-6000, 6000, 100) 同上。
X, Y = np.meshgrid(x_r, y_r) 使用np.meshgrid函數來產生網格,用於繪製曲面。
Z = fit_equation((X, Y), *popt) 根據擬合出來的曲面fit_equation來計算網格座標(X, Y)對應的 Z 值。
ax.plot_surface(X, Y, Z, color=’red’, alpha=0.2) 在3D subplot上繪製擬合曲面,color=’red’指定擬合曲面以紅色顯示,alpha=0.2則表示此曲面的透明度為0.2。
ax.set_xlabel(‘X’)、ax.set_ylabel(‘Y’)和ax.set_zlabel(‘Z’) 指定3D subplot的座標軸標籤。
plt.show() 輸出繪製的圖形。
完整的程式碼為
import pandas as pd
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
df = pd.read_csv('data.csv')
x = df.iloc[:, 0]
y = df.iloc[:, 1]
z = df.iloc[:, 2]
data = np.array([x, y, z]).T
def fit_equation(xy, a, b, c, d, e, f):
x, y = xy
return a*x + b*y + c*x*x + d*y*y + e*x*y + f
popt, pcov = curve_fit(fit_equation, (x, y), z)
print(popt)
#有繪圖需求才需要下列的程式碼
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, color='blue')
x_r = np.linspace(-6000, 6000, 100)
y_r = np.linspace(-6000, 6000, 100)
X, Y = np.meshgrid(x_r, y_r)
Z = fit_equation((X, Y), *popt)
ax.plot_surface(X, Y, Z, color='red', alpha=0.2)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
如果要把擬合曲面畫成類似漁網的效果,將倒數第五行改成
ax.plot_wireframe(X, Y, Z, color='red', alpha=0.2, rstride=10, cstride=10)
可以得到